Physical intuitions for impedance matching and critical damping

This semester I took an introductory class on electrical circuit analysis. One of the concepts introduced was impedance matching: the idea that if you want to deliver maximum power to a load, the amount that the load “pushes back” on the power source should be equal to (the complex conjugate of) the amount the rest of the circuit pushes back. If you were writing a textbook, you would convince your readers like so:

But what if you weren’t writing a textbook, and wanted to convince someone who was planning on simply getting up and walking away the moment any of those libertine little d’s or, god forbid, the imaginary unit (or the jmagjnary unjt, as the case may be) made an appearance?

Then you could say, imagine you are playing that game where you put a jump rope on the ground and send a pulse through it. You want to try to make sure that the pulse that reaches some given point on the jump rope is, as precisely as possible, exactly the same as the pulse that leaves your hand. You have two choices.

First, you could use two jump ropes tied together, where the two ropes have different thicknesses, or might be made of different materials, or maybe one of them is that beaded kind that hurts like a #!%$ when you hit yourself in the ankle with it:

Or your second option, you could just use one really long jump rope, that has the same thickness and material used throughout.

It’s intuitively obvious that, if there’s a possibility of you being asked to transmit that as-faithful-as-possible pulse to the far side of the rope, you’re way better off with the one long rope. If that isn’t obvious, it’s obvious that you can go buy some jump ropes and try it out for yourself. Of course, the rope that has the same “impedance” throughout is going to transmit the pulse more faithfully, while the tied-together bit is going to muck things up.

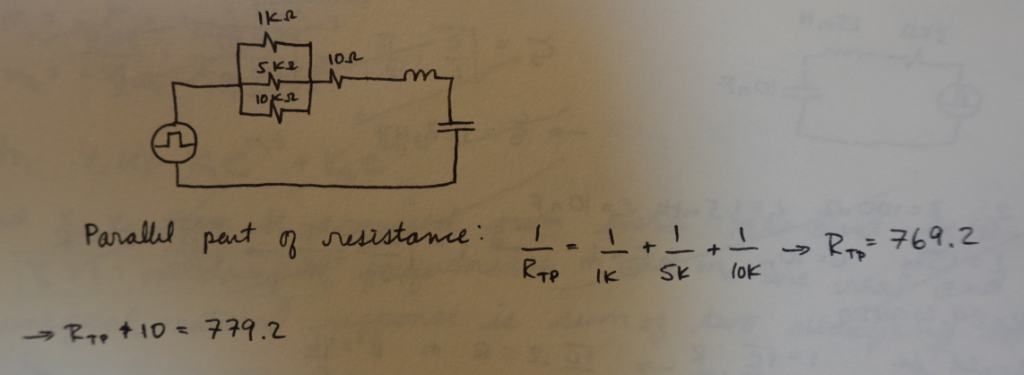
A piece of physical intuition that was less obvious to me at first was that for critical damping. In one assignment, we simulated in software and built in meatspace three different versions of an LRC circuit: an underdamped one, overdamped one, and then figuring out what resistive value to swap in to get it critically damped.

Of course, an underdamped circuit oscillates, as seen in both the simulation and the oscilloscope hooked up to a breadboard:

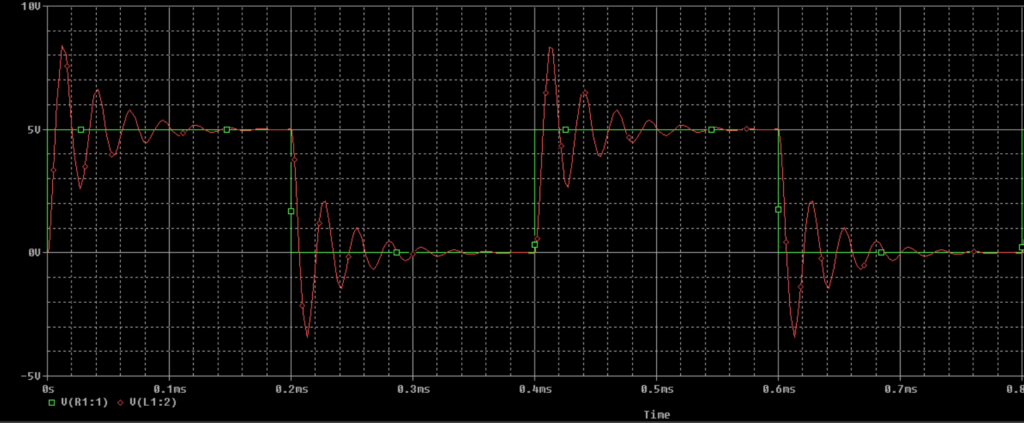
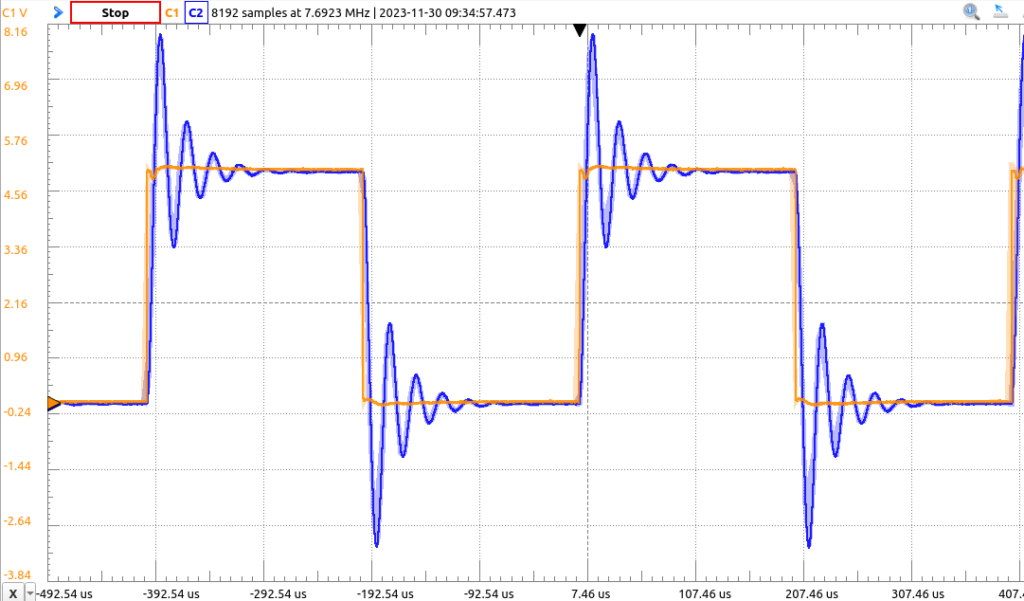
And an overdamped circuit decays exponentially:

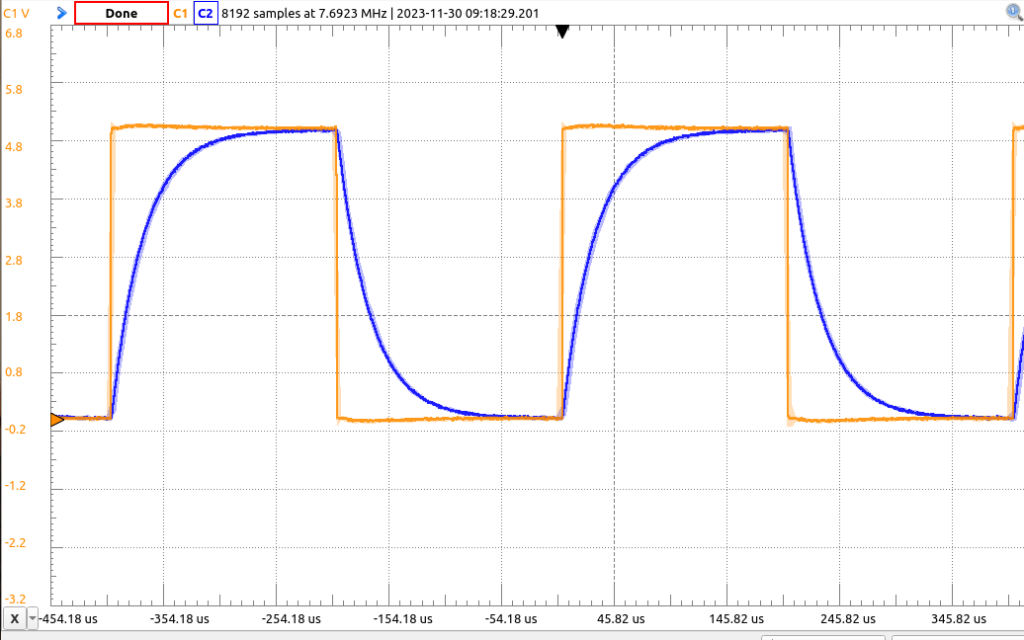
A critically damped circuit– i.e., one where the characteristic equation of the circuit has repeated roots, and there is only one natural frequency– decays faster than an overdamped one:

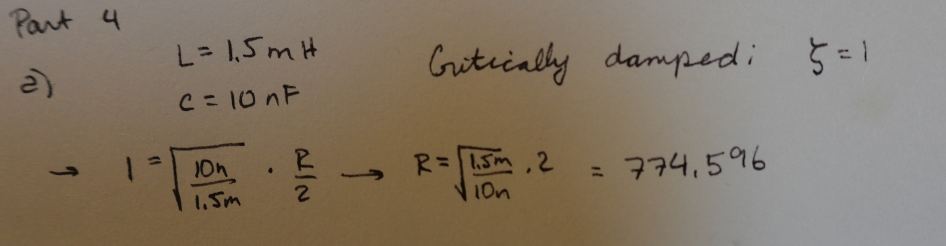
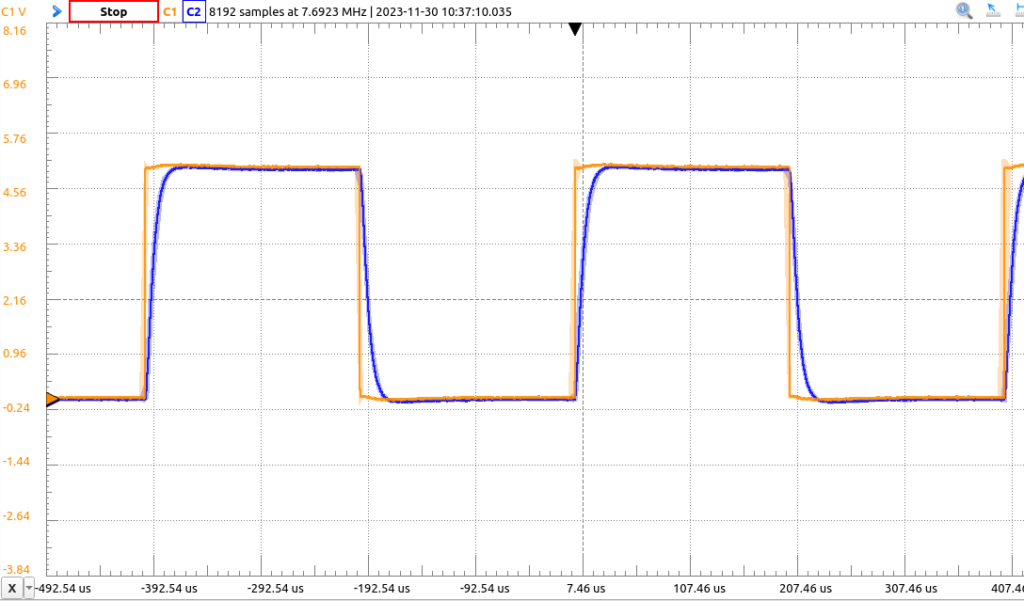
Why, though? When the words are spoken, it sounds like the thing called “overdamped” should do the thing called “decaying” the fastest. The math, of course, is entirely clear: with repeated roots to the characteristic equation, the solution to the differential equation has an exponential decay term multiplied by the independent variable of time, while the overdamped case has no such thing. So of course the critically damped case has to decay faster. But that’s just a property of multiplication, not a good explanation (and we lost the no-libertine-d’s-or-i’s-or-j’s observer some time ago.)

The physical intuition, then: imagine you are dropping a little ball into a glass of some kind of fluid. Your goal is for the ball to come to rest on the bottom of the glass– equilibrium– as quickly as possible. If the fluid is not sticky enough to slow down the ball before it hits the bottom, it will bounce (underdamped.) If the fluid is sticky, it will slow down the ball enough that it won’t bounce– but there is a point of stickiness beyond which any extra stickiness isn’t actually helping to prevent bounces, it’s just delaying the ball reaching the bottom. Just the right stickiness to prevent bouncing, without slowing down the ball’s progress more than necessary, is critical damping; excessive stickiness is overdamping.